Obtaining the potential energy of a given configuration of atoms is the keystone of almost all material science research. A phase is a macroscopic manifestation of that atomic structure of it's constituents to a degree of coarseness such that it is chemically distinct and mechanically separable. Now the observed phase (ergo the internal structure) for a given chemical composition of elements (alloys/compounds) is governed by the laws of thermodynamics which states that the stable and observed phase is that which has the minimum potential energy. Going forward with the knowledge of the observed phase translates theoretical foundations to engineering applications since the phase dictates the properties of the phase (electrical, mechanical, chemical etc.) which then finds its place in the appropriate use case.
The fundamental equation which maps configurations to energy is the eponymous Schrodingers Wave Equation (SE). However, real world bulk materials contain atoms to the order of $10^{23}$ and since the solution to SE has a complexity of $\mathcal{O}(N^2)$, the true solution becomes intractable pretty fast. An approximate solution to the problem is using Density Functional Theory, which treats the interaction of each particle with an overall local atomic density which is a combination of all the other particles (instead of considering each particle individually as in the full solution). This too unfortunately gets out of hand beyond systems of more than couple 1000 atoms. Traditionally, to overcome this scale problem, several (approximate) methods were developed at different length scales that satisfy the engineering requirements at that scale. Phase Field Modelling, Classical Molecular Dynamics, Dislocation Dynamics, Micro-mechanics, Finite Element Modelling are some of the available techniques in increasing order of magnitude of length.
In this article, we shall limit our focus to the discussion of a bridge of sorts between the atomistic calculations (via DFT) to classical molecular dynamics. In reality, atoms behave according the wave-particle duality as predicted by quantum mechanics (SE is the workhorse behind quantum mechanics), however, within acceptable accuracy, it is possible to assume the behaviour of atoms like classical molecules obeying Newton's Laws. The subtlety is in the choice of the energy field in which these particles operate. Although exact functional forms differ according to the energy model, the gist of all these models is the interaction of a single atom with a effective potential from the aggregation of all other particles in the system.
The modus operandi of construction of these fitted energy models is what is known as the potential energy surface (PES) construction. It is an arduous task since most of these are constructed to reproduce select physical constants as per the researchers interest and is not transferable to other calculations. Often it involves iterating the fit over select regions of interest. A few very accurate calculations are done on well sampled space of configurations and then those energies are fitted to a pre-determined functional form to interpolate the entire landscape. Traditionally, the complexity of interactions range from simple pair-potentials (like lennard-jones) to many-body interactions (EAM) and beyond. However, since the models are just empirical, there are in principle infinite forms that the data could be fitted to provided they satisfy certain natural constraints. In summary, the problem at hand is a non-linear high-dimensional constrained optimisation problem (something that ML methods in are very adept at representing)
Let's discuss the aforementioned constraints. From principles of physics, it is well known, that the energy of a configuration remains invariant under the action of translation, pure rotation, pure reflection and all permutations that preserve the space group. A configuration is originally defined by a set of vectors of atom positions. Unfortunately, the cartesian representation does not preserve the physical symmetries. Thus it is import to recast the configuration in an alternative set of descriptors that maintain the symmetries yet gives an unique and unequivocal representation to the configuration under consideration.
Once we settle on the descriptor, we can then choose appropriate fitting strategy to map those descriptors to the associated energy. In the following sections, we shall discuss some of these descriptors and also some methods that fit energy as a function of descriptorsy. It might be a good time to stress that these methods, although are different in their functional forms, the spirit of the calculations are all similar in a certain fashion. $$ \begin{align*} E &= \sum_n \epsilon(q_1^{(n)},\cdots,q_m^{(n)}) \end{align*} $$ where $E$ is the total energy of the configuration, which is the sum total of the energy of n atoms. Each atom has an energy $\epsilon_n$, which is function of $(q_1^{(n)},\cdots,q_m^{(n)})$, the set of descriptor characterising the local atomic environment. A more precise formulation for each of the $\epsilon(q)$ is therefore expressed as a weighted sum of a fixed non-linear kernel function but with every other descriptor $$ \begin{equation} \label{eqn1}\tag{1} \epsilon(q) = \sum_{k=1}^N \alpha_k K(q,q^{(k)}) \end{equation} $$ where N is the dimension of the descriptor spaces, which we can throw at any fitting mechanism to obtain $\alpha \equiv (\alpha_1,\cdots,\alpha_N)$.
We can interpret the K's as a measure of similarity between the configuration whose energy we are interested in and the configurations whose energy we have calculated through more accurate methods in a higher dimensional space than that of the descriptor. This here is the key concept that connects ML paradigms to the construction of a PES.
The descriptors will also be limited to those that can be applied to periodic systems. The discussion is no way exhaustive, rather the ones I know of in my short literature review. However all of these also have code implementations available online so it shouldn't be very difficult to get hands wet on any of these techniques.
Descriptors
Parrinello-Behler descriptor (Atom Centred Symmetry functions)
In this method, each atoms position is represented as a set of spherical symmetry function, which is basically a smooth symmetric function of it's distance with neighbouring atoms up to a cut-off distance where the functions smoothly vanish to zero. This preserves symmetry as well as relaxes the need to maintain a sort of nearest neighbours list all time. The functions are: $$ \begin{align*} G_i^1 &= \sum_j f_c(R_{ij})\\ G_i^2 &= \sum_j e^{-\eta(R_i - R_j)}f_c(R_{ij})\\ G_i^3 &= \sum_j \cos(\kappa R_{ij})f_c(R_{ij})\\ G_i^4 &= 2^{1-\xi}\sum_{j,k\neq i}^{all}(1+\lambda\cos\theta_{ijk})^\xi\cdot e^{-\eta(R_{ij}^2 + R_{jk}^2 + R_{ik}^2)}\cdot f_c(R_{ij})\cdot f_c(R_{jk})\cdot f_c(R_{ik})\\ G_i^5 &= 2^{1-\xi}\sum_{j,k\neq i}^{all}(1+\lambda\cos\theta_{ijk})^\xi\cdot e^{-\eta(R_{ij}^2 + R_{ik}^2)}\cdot f_c(R_{ij})\cdot f_c(R_{ik})\\ \end{align*} $$ The cut-off function used is $$ f_c(R_{ij}) = \begin{cases} \frac{1}{2}\left[\cos\left(\frac{\pi R_{ij}}{R_c}\right) + 1\right] & \mbox{for } R_{ij} \leq R_c\\ 0 & \mbox{for } R_{ij} > R_c \end{cases} $$ Function $G^1$ is just the sum of the cut-off functions for all the neighbours. $G^2$ are shifted Gaussians multiplied by cut-off which can describe a spherical shell around the reference atom. $G^3$ is a damped cosine, there can me multiple description of $G^3$ by combinations of different $\kappa$ values. This is a case of over complete set of descriptors, but still there is no ambiguity between different real configurations.
Function $G^4$ and $G^5$ have the angular functions where $\theta_{ijk} = acos \left(\frac{R_{ij} \cdot R_{ik}}{|R_{ij} \cdot R_{ik}|}\right)$. The maxima of the cosine function can be shifted from $\theta_{ijk} = 0$ to $\theta_{ijk} = 180^\circ$ depending on the $\lambda$ parameter. $\xi$ controls the width of the symmetry functions around its centre. The distance can also be tuned by the $\eta$ and R$_c$ parameter.
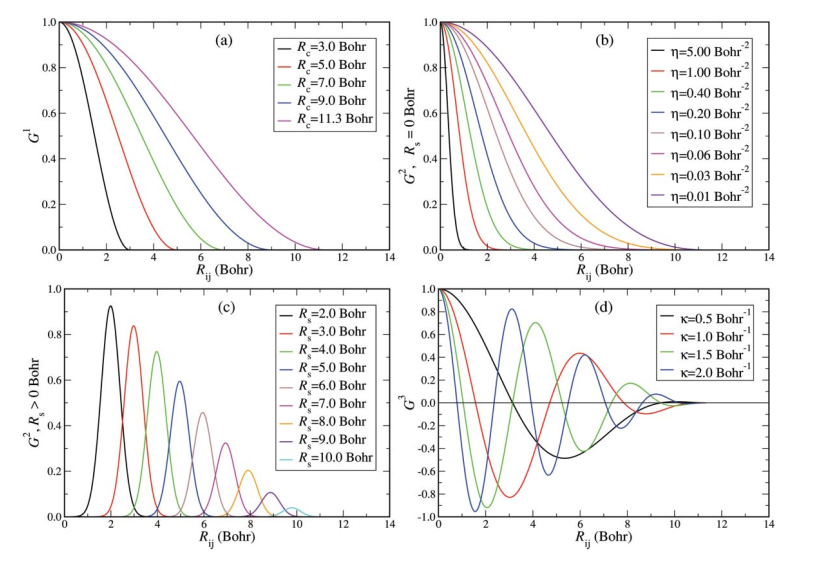
The authors have used Neural Networks to fit the energy functional. As we shall discuss later, this treatment make it amenable to have analytic gradients, which can be used to calculate forces and stress tensor as required by an MD or meta-dynamics for crystal structure prediction.
Bispectrum - A generalised power spectrum
The first step of the invariant transformation descriptor is to calculate the atomic neighbour density function as $$ \rho_i(R) = \delta (R) + \sum_{ R_{ij} < R_c} f_c(R_{ij}) w_{Z_i}\delta (R - R_{ij}) $$ where $i$ runs up to a cut-off distance. $w_{Z_i}$ is an unique weight factor to distinguish different species.
At first, we expand every point on the unit sphere pointing at R (basically considering the angular part only), we express the atomic density is terms of it spherical harmonics. $$ \rho(\theta,\phi) = \sum_{l=0}^\infty\sum_{m=-l}^l c_{lm}Y_{lm}(\theta,\phi) $$ where, $$ c_{lm} = \left<\rho|Y_{lm}\right> = \sum_i Y_{lm}(\theta,\phi) $$ Let's define, $Q_l = \frac{1}{N}\sum_i Y_{lm}(\theta,\phi)$, this is already permutation and translationally invariant, but depend on the orientation of the reference frame. However from that we can construct a set of rotationally invariant combinations by $$ \begin{align} Q_l &= \left[\frac{4\pi}{2l+1}\sum_{m=-l}^l Q_{lm}^*Q_{lm}\right]^{1/2} \mbox{and }\\ W_l &= \sum_{m_1,m_2,m_3 = -l}^l \begin{pmatrix}l & l & l \\ m_1 & m_2 & m_3\end{pmatrix}Q_{lm_1}Q_{lm_2}Q_{lm_3} \end{align} $$ The factor in parentheses are the Wigner 3 $jm$ symbol
Power Spectrum
We can also prove that the power series $p_l = c_l^Tc_l$ is also rotationaally invariant and is related to $Q_l$ as $$ Q_l = \left(\frac{4\pi}{2l+1}p_l\right)^{1/2} $$
Bispectrum
However the power series is far from mundane, since a more richer set of invariants can be obtained by coupling the different angular channels. Let us define $$ C^{l_1l_2}(c_1\otimes c_2) \equiv \bigoplus_{l=|l_1 - l_2|}^{l_1+l_2}g_{ll_1l_2} $$ then $$ b_{ll_1l_2} = c_l^Tg_{ll_1l_2} $$ is rotationally invariant. This is known as the bispectrum component. If we further want invariance to reflection, we either take the absolute value or zero out the elements of the bispectrum where $l_1 + l_2 + 1$ is odd (as it changes sign during reflection).
We can rewrite the bispectrum formula as $$ b_{ll_1l_2} = \sum_{m=-l}^l\sum_{m=-l_1}^{l_1}\sum_{m=-l_2}^{l_2} c_lm^*C_{mm_1m_2}^{ll_1l_2}c_{l_1m_1}c_{l_2m_2} $$ where is the evidently similar to third-order bond-order parameters. In fact, the Wigner 3$jm$ symbol and the Clebsch-Gordan coefficients are related by $$ \begin{pmatrix}l_1 & l_2 & l_3 \\ m_1 & m_2 & m_3\end{pmatrix} = \frac{(-1)^{l_1-l_2-m_3}}{\sqrt{2l_3+1}}C^{l_1l_2l_3}_{m_1m_2-m_3} $$
Radial Basis Functions
We can further add radial dependence, by modifying the atomic density with a radial basis function $g_n(r)$, such that $$ \rho(r) = \sum_n\sum_{l=0}\sum_{m=-l}^lc_{nlm}g_n(r)Y_{lm}(\theta,\phi) $$ such that $\left< g_n|g_m \right> = S_{nm} \neq \delta_{nm}$, going forward as before $$ \begin{align*} c_{nlm}' &= \left< g_nY_{lm}|\rho \right> \mbox{and}\\ c_{nlm} &= \sum_{n'}(S^{-1})c_{n'lm}' \end{align*} $$
The power spectrum and bispectrum can be similarly calculated as $$ \begin{align*} p_{nl} &= \sum_{m=-l}^lc_{nlm}^*c_{nlm}\\ b_{nll_1l_2} &= \sum_{m=-l}^l\sum_{m=-l_1}^{l_1}\sum_{m_-l_2}^{l_2}c^*_{nlm}C^{ll_1l_2}_{mm_1m_2}c_{nl_1m_1}c_{nl_2m_2} \end{align*} $$
4 dimensional Power spectrum and Bispectrum
Another representation that does not need an explicit radial function is by extending the representation in spherical harmonics of 4 dimension in a fixed hypersphere of radius $r_o$. The mapping of the Cartesian to 4-D polar coordinates is therefore $$ \begin{pmatrix} x \\ y\\ z\end{pmatrix} \rightarrow \begin{pmatrix} \phi = \tan^{-1} y/x \\ \theta = \cos^{-1} z/|r|\\ \theta_o = \pi |r|/r_o\end{pmatrix} $$
Any point can then be expanded into hyperspherical harmonics as $$ \rho = \sum_{j=0}^\infty\sum_{m,m'=-j}^jc_{m,m'}^jU_{m,m'}^j $$ where, $c_{m,m'}^j = \left< U_{m,m'}^j|\rho\right>$
As in the 3D case, the bispectrum elements of for the SO(4) groups are $$ B_{jj_1j_2} = \sum_{m_1',m_1=-j_1}^{j_1} c_{m'_1m_1}^{j_1} \sum_{m_2',m_2=-j_2}^{j_2} c_{m'_2m_2}^{j_2} \times \sum_{m',m=-j} C_{mm_1m_2}^{jj_1j_2}C_{m'm'_1m'_2}^{jj_1j_2}(c_{m'm^j}*) $$ while the SO(4) power spectrum is $$ P_j = \sum_{m',m=-j}^j (c_{m',m}^j)^*c_{m'm}^j $$
These descriptors besides having physical significance are also systematically improvable based on the the application requirements. Although the description is not complete in principle, the class of functions such as sum of finite number of delta functions (such as the atomic neighbour density) it can be demonstrated that the particular set of description is likely over-complete.
SOAP - Smooth Overlap of Atomic Positions
In the introduction we said that the potential energy of ultimately is function of the kernel which is a measure of similarity between two configurations and lives on the descriptor space. Therefore it is a logical conclusion that if we can bypass the construction of a descriptor but get straight to a kernel function, the fit should work equally well. That is the principle idea behind SOAP
Let's define a similarity function directly, $$ S(\rho,\rho ') = \int \rho(r)\rho '(r)dr $$ This is a permutational and translational invariant, integrating it along all possible rotation on one of the environment leads to the kernel $$ \begin{align*} K(\rho,\rho ') &= \int |S(\rho,R\rho ')dR\\ &= \int dR \left|\int \rho(r)\rho '(Rr)dr\right|^n \end{align*} $$
To analytically evaluate the above integral, let's take an atomic neighbour density as a sum of Gaussian centred on each atom (instead of earlier delta functions) $$ \rho(r) = \sum_i \exp (-\alpha|r - r_i|^2) = \sum_i\sum_{lm}c^i_{lm}(r)Y_{lm}(\hat{r}) $$ where $$ c^i_{lm} \equiv 4\pi\exp[-\alpha (r^2 - r_i^2)]\iota_l (2\alpha rr_i)Y^*_{lm}(\hat{r_i}) $$ and $\iota_l$ is the modified Bessel function of the first kind.
Further defining $$ \tilde{I}^l_{mm'}(\alpha,r_i,r_{i'}) = 4\pi\exp[-\alpha (r_i^2 - r_{i'}^2)/2]\iota_l (2\alpha r_ir_{i'})Y_{lm}(\hat{r_i})Y^*_{lm}(\hat{r_{i'}}) $$ and $$ I^l_{mm'} \equiv \sum_{i,i'}\tilde{I}^l_{mm'}(\alpha,r_i,r_{i'}) $$
For n = 2, we get a rotationally invariant kernel as $$ k(\rho,\rho ') = \sum_{lmm'} (I^l_{mm'})^*I^l_{mm'} $$ and for n = 3, we get $$ k(\rho,\rho ') = \sum I^{l_1}_{m_1m_1'} I^{l_2}_{m_2m_2'} I^l_{mm'} C^{lm}_{l_1l_2m_1m_2} C^{lm'}_{l_1l_2m_1'm_2'} $$
Then we can describe the SOAP kernel as $$ K(\rho,\rho ') = \left(\frac{k(\rho,\rho ')}{\sqrt{k(\rho,\rho)k(\rho ',\rho ')}}\right)^\xi $$ where $\xi$ is any positive integer.
Now if we add a radial basis function to the spherical harmonic expansion of the atomic neighbour density, the kernel (for n = 2) can be expressed as $$ k(\rho,\rho ') \equiv \sum_{nn'l}p_{nn'l}p_{nn'l}' $$ Analogously for n = 3, $$ k(\rho,\rho ') \equiv \sum_{n_1n_2n\\l_1l_2l} b_{n_1n_2nll_1l_2}b_{n_1n_2nll_1l_2}' $$ where $$ b_{n_1n_2nl_1l_2l} \equiv \sum c_{n_1l_1m_1}c_{n_2l_2m_2}(c_{nlm})^*C_{l_1m_1l_2m_2}^{lm} $$
'The above equations expose that the SOAP kernel is equivalent to the SO(3) bispectrum descriptor along with a Gaussian atomic neighbour density function and a dot product covariance kernel. Although this is the same technique as before, the SOAP methodology eliminates the need for the introduction of some ad hoc choices, while giving sufficient control via the $\alpha$ and $\xi$ hyperparameters.
ML Potentials
In the previous section, we discussed the different descriptors of a configuration which preserves the essential materials symmetry. In this section, we shall see discuss the techniques that map those descriptors to the required energy. Although in principle the descriptors are independent of the strategy used to obtain the energy, researchers have traditionally paired descriptors with their choice of techniques. Since the development of both were done by same researcher, some descriptors follow a natural association to a fitting strategy.
Artificial Neural Networks
Artificial Neural Networks (ANN/NN) is the oldest ML fitting technique. To the best of my knowledge, the best results were obtained in conjunction with ACSF (Behler-Parinello) descriptors. The image below gives a toy structure for a NN model, where on the left, the inputs are the different sets of descriptors $G_i$ as defined by ACSF, while on the right we obtain the potential energy E for that given set of $G_i$s
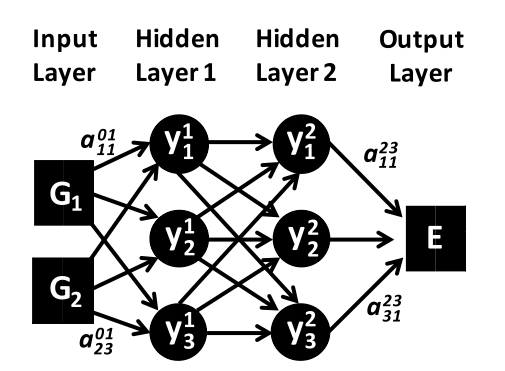
For the above diagram, the analytic form of the potential energy E is given by $$ E = f\left(b_1^3 + \sum_{k=1}^3 a_{k1}^{23} \cdot f\left(b_k^2 + \sum_{j=1}^3 a_{jk}^{12} \cdot f\left(b_j^1 + \sum_{i=1}^2 G_i \cdot a_{ij}^{01}\right)\right)\right) $$ Where $b_i^j$ are biases, which are tunable offsets to the activations of a layer that are determined by weights $a_{ij}^{kl}$ that are the fitting parameters relating the ith node of the jth layer to the kth node of the jth layer. $f()$ are the non-linearities to the activations, which are traditionally hyperbolic tangents or Gaussian's.
Gaussian Approximation Potentials (GAP)
GAP potentials are an umbrella term for a general class of potentials where the energy of a configuration is a function of a kernel formed by bispectrum components using Gaussian Process Regression $$ \begin{align*} E_i &= \sum_{n=1}^{N_{\text{ref}}} \alpha_n e^{-0.5\sum_{l=1}^L[(b_l-b_{n,l})/\theta_l]^2}\\ &= \sum_{n=1}^{N_{\text{ref}}} \alpha_ne^{G(b,b_n)} \end{align*} $$ where L is the total number of components of the bispectrum and $\theta_l$ are the fitting parameters.
The GAP formalism could also be extended to SOAP kernel and SO(4) bispectrum descriptors
Spectral Neighbour Analysis Potential (SNAP)
SNAP is the linear approximation of GAP. Here the atomic energy is expressed as a linear sum of the bispectrum components (truncated at L) $$ E_{i,\text{SNAP}} = \beta_o^{\alpha_i} + \sum_{l=1}^L \beta_l^{\alpha_i} \cdot b_k^i $$ where $\alpha_i$ describes the specific atom time of $i$, $b_k^i$ is the kth bispectrum component of atom i and $\beta_o^{\alpha_i}$ is the constant element specific contribution.
The SNAP energy due to its analytical form can also be explicitly differentiated to obtain forces and stress-tensors.
Implementations
- DScribe: https://singroup.github.io/dscribe/latest/#
Python package to generate SOAP and ACSF descriptors. -
Quippy: https://github.com/libAtoms/QUIP
Fortran package to fit GAP potentials. - RuNNer: https://www.uni-goettingen.de/de/560580.html
The NN PES code by Joerg Behler. - LAMMPS: https://lammps.sandia.gov/doc/pair_snap.html
Support SNAP potentials
References
- General Review 1: A. P. Bartók, R. Kondor, and G. Csányi, Phys. Rev. B 87, 184115 (2013)
- General Review 2 and SOAP: J. Behler, J. Chem. Phys. 145, 170901 (2016)
- Embedded Atom Method (EAM): M. S. Daw, S. M. Foiles and M. I. Baskes, Mater. Sci. Rep, 9 (1993)
- Atom Centred Symmetry Functions: J. Behler, J. Chem. Phys. 134, 074106 (2011)
- Bispectrum: A. P. Bartók, M. C. Payne, R. Kondor, and G. Csányi, Phys. Rev. Lett. 104, 136403 (2010)
- GAP: A. P. Bartók, and G. Csányi, Int. J. Quantum Chem, 115, (2015)
- ANN: J. Behler and M. Parrinello, Phys. Rev. Lett. 98, 146401 (2007).
- SNAP: A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles, and G. J. Tucker, J. Comput. Phys. 285, 316 (2015).